Function Reference: qsmmmk

Function File: [U, R, Q, X, p0, pK] = qsmmmk (lambda, mu, m, K)
Function File: pn = qsmmmk (lambda, mu, m, K, n)

Compute utilization, response time, average number of requests and throughput for a M/M/m/K finite capacity system. In a M/M/m/K system there are m \geq 1 identical service centers sharing a fixed-capacity queue. At any time, at most K ≥ m requests can be in the system, including those being served. The maximum queue length is K-m. This function generates and solves the underlying CTMC.

$$ \pi_n = \cases{ \displaystyle{{\rho^n \over n!} \pi_0} & if $0 \leq n \leq m$;\cr\cr \displaystyle{{\rho^m \over m!} \left( \rho \over m \right)^{n-m} \pi_0} & if $m < n \leq K$\cr} $$$$ \pi_0 = \left[ \sum_{k=0}^m {\rho^k \over k!} + {\rho^m \over m!} \sum_{k=m+1}^K \left( {\rho \over m}\right)^{k-m} \right]^{-1} $$

INPUTS

lambda

Arrival rate (lambda>0)

mu

Service rate (mu>0)

m

Number of servers (m ≥ 1)

K

Maximum number of requests allowed in the system, including those being served (K ≥ m)

n

Number of requests in the (0 ≤ n ≤ K).

OUTPUTS

U

Service center utilization

R

Service center response time

Q

Average number of requests in the system

X

Service center throughput

p0

Steady-state probability that there are no requests in the system.

pK

Steady-state probability that there are K requests in the system (i.e., probability that the system is full).

pn

Steady-state probability that there are n requests in the system (including those being served).

If this function is called with less than five arguments, lambda, mu, m and K can be either scalars, or vectors of the same size. In this case, the results will be vectors as well.

REFERENCES

  • G. Bolch, S. Greiner, H. de Meer and K. Trivedi, Queueing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications, Wiley, 1998, Section 6.6

See also: qsmm1, qsmminf, qsmmm

Example: 1

  

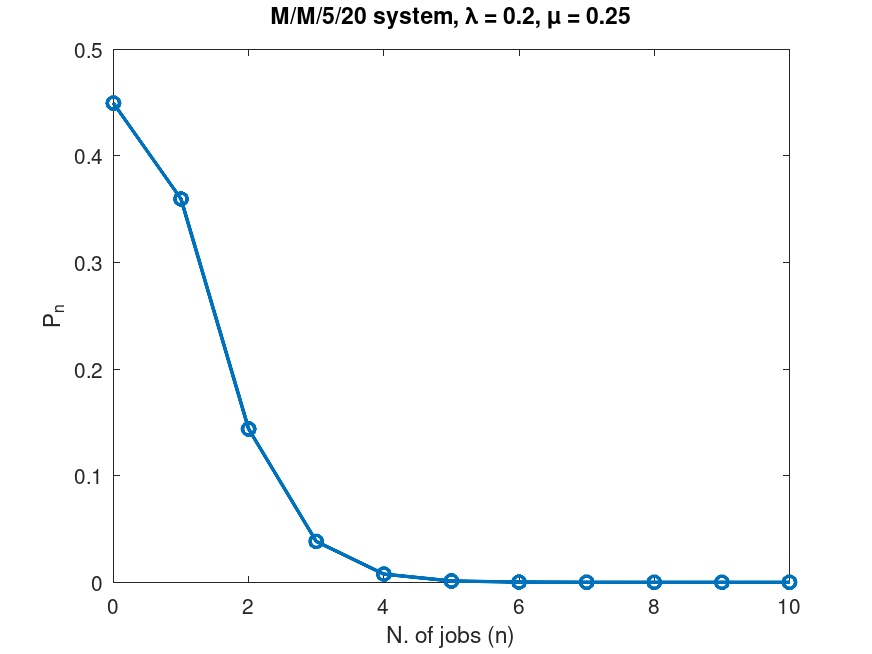
 ## Given a M/M/m/K queue, compute the steady-state probability pn
 ## of having n jobs in the systen.
 lambda = 0.2;
 mu = 0.25;
 m = 5;
 K = 20;
 n = 0:10;
 pn = qsmmmk(lambda, mu, m, K, n);
 plot(n, pn, "-o", "linewidth", 2);
 xlabel("N. of jobs (n)");
 ylabel("P_n");
 title(sprintf("M/M/%d/%d system, \\lambda = %g, \\mu = %g", m, K, lambda, mu));
plotted figure