Function Reference: qsmmm

Function File: [U, R, Q, X, p0, pm] = qsmmm (lambda, mu)
Function File: [U, R, Q, X, p0, pm] = qsmmm (lambda, mu, m)
Function File: pk = qsmmm (lambda, mu, m, k)

Compute utilization, response time, average number of requests in service and throughput for a M/M/m queue, a queueing system with m identical servers connected to a single FCFS queue.

$$ \pi_k = \cases{ \displaystyle{\pi_0 { ( m\rho )^k \over k!}} & $0 \leq k \leq m$;\cr\cr \displaystyle{\pi_0 { \rho^k m^m \over m!}} & $k>m$.\cr } $$$$ \pi_0 = \left[ \sum_{k=0}^{m-1} { (m\rho)^k \over k! } + { (m\rho)^m \over m!} {1 \over 1-\rho} \right]^{-1} $$

INPUTS

lambda

Arrival rate (lambda>0).

mu

Service rate (mu>lambda).

m

Number of servers (m ≥ 1). Default is m=1.

k

Number of requests in the system (k ≥ 0).

OUTPUTS

U

Service center utilization, U = \lambda / (m \mu).

R

Service center mean response time

Q

Average number of requests in the system

X

Service center throughput. If the system is ergodic, we will always have X = lambda

p0

Steady-state probability that there are 0 requests in the system

pm

Steady-state probability that an arriving request has to wait in the queue

pk

Steady-state probability that there are k requests in the system (including the one being served).

If this function is called with less than four parameters, lambda, mu and m can be vectors of the same size. In this case, the results will be vectors as well.

REFERENCES

  • G. Bolch, S. Greiner, H. de Meer and K. Trivedi, Queueing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications, Wiley, 1998, Section 6.5

See also: erlangc, qsmm1, qsmminf, qsmmmk

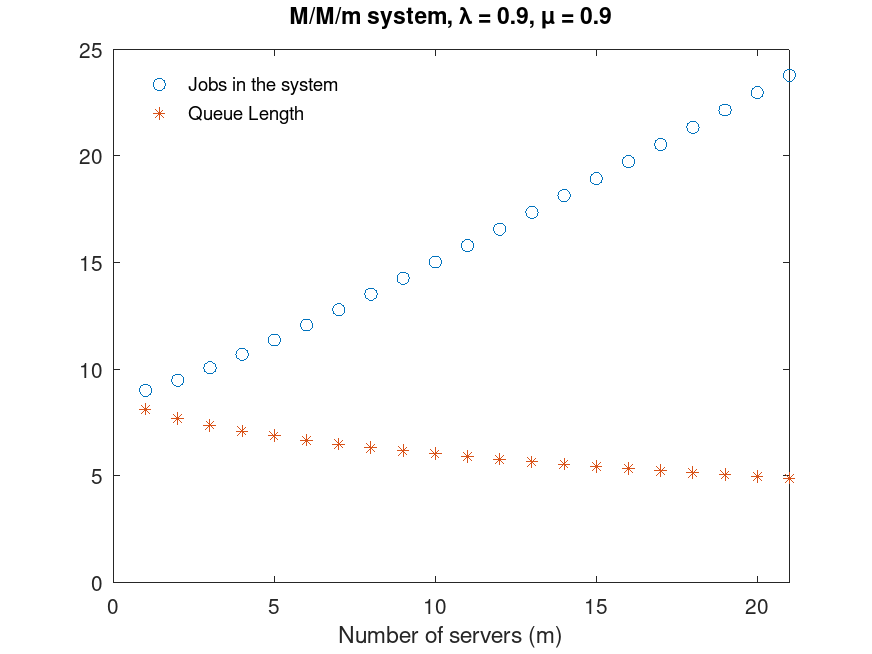
Example: 1

  

 # This is figure 6.4 on p. 220 Bolch et al.
 rho = 0.9;
 ntics = 21;
 lambda = 0.9;
 m = linspace(1,ntics,ntics);
 mu = lambda./(rho .* m);
 [U R Q X] = qsmmm(lambda, mu, m);
 qlen = X.*(R-1./mu);
 plot(m,Q,"o",qlen,"*");
 axis([0,ntics,0,25]);
 legend("Jobs in the system","Queue Length","location","northwest");
 legend("boxoff");
 xlabel("Number of servers (m)");
 title("M/M/m system, \\lambda = 0.9, \\mu = 0.9");
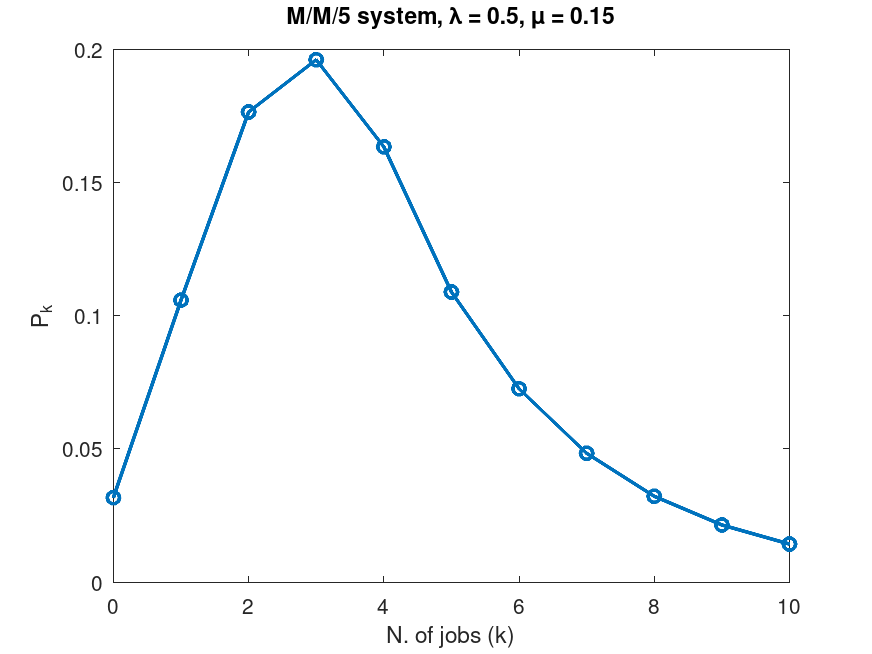
plotted figure

Example: 2

  

 ## Given a M/M/m queue, compute the steady-state probability pk of
 ## having k jobs in the systen.
 lambda = 0.5;
 mu = 0.15;
 m = 5;
 k = 0:10;
 pk = qsmmm(lambda, mu, m, k);
 plot(k, pk, "-o", "linewidth", 2);
 xlabel("N. of jobs (k)");
 ylabel("P_k");
 title(sprintf("M/M/%d system, \\lambda = %g, \\mu = %g", m, lambda, mu));
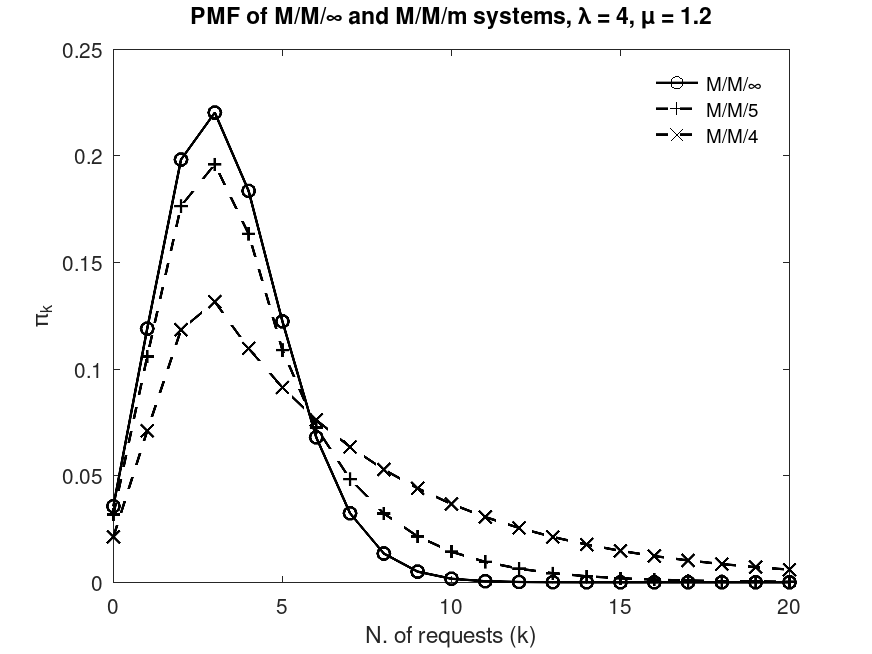
plotted figure

Example: 3

  

 ## This code produces Fig. 4 from the paper: M. Marzolla, "A GNU
 ## Octave package for Queueing Networks and Markov Chains analysis",
 ## submitted to the ACM Transactions on Mathematical Software.

 lambda = 4; mu = 1.2;
 k = 0:20;
 pk_inf = qsmminf(lambda, mu, k);
 pk_4 = qsmmm(lambda, mu, 4, k);
 pk_5 = qsmmm(lambda, mu, 5, k);

 plot(k, pk_inf, "-ok;M/M/\\infty;", "linewidth", 1.5, ...
      k, pk_5, "--+k;M/M/5;", "linewidth", 1.5, ...
      k, pk_4, "--xk;M/M/4;", "linewidth", 1.5 ...
     );
 xlabel("N. of requests (k)");
 ylabel("\\pi_k");
 legend("boxoff");
 title(sprintf("PMF of M/M/\\infty and M/M/m systems, \\lambda = %g, \\mu = %g", lambda, mu));
plotted figure