Function Reference: qnom
- Function File: [U, R, Q, X] = qnom (lambda, S, V)
- Function File: [U, R, Q, X] = qnom (lambda, S, V, m)
- Function File: [U, R, Q, X] = qnom (lambda, S, P)
- Function File: [U, R, Q, X] = qnom (lambda, S, P, m)
Exact analysis of open, multiple-class BCMP networks. The network can be made of queueing centers (FCFS, LCFS-PR or PS) or delay centers (IS). This function assumes a network with service centers and customer classes.
INPUTS
-
lambda(c)
If this function is invoked as qnom(lambda, S, V, …),
then lambda(c) is the external arrival rate of class
customers (lambda(c) ≥ 0). If this
function is invoked as qnom(lambda, S, P, …), then
lambda(c,k) is the external arrival rate of class
customers at center (lambda(c,k)
≥ 0).
S(c,k) mean service time of class customers on the service center
(S(c,k)>0). For FCFS nodes, mean service
times must be class-independent.
V(c,k) visit ratio of class customers to service center
(V(c,k) ≥ 0 ). If you pass this argument,
class switching is not allowed
P(r,i,s,j) probability that a class job completing service at center
is routed to center as a class job.
If you pass argument P, class switching is allowed;
however, all servers must be fixed-rate or infinite-server nodes
(m(k) ≤ 1 for all ).
m(k) number of servers at center . If m(k) < 1,
enter is a delay center (IS); otherwise it is a regular
queueing center with m(k) servers. Default is
m(k) = 1 for all .
OUTPUTS
-
U(c,k)
If is a queueing center, then U(c,k) is the
class utilization of center . If is an IS
node, then U(c,k) is the class defined as X(c,k)*S(c,k).
R(c,k) class response time at center . The system
response time for class requests can be computed as
dot(R, V, 2).
Q(c,k) average number of class requests at center . The
average number of class requests in the system Qc
can be computed as Qc = sum(Q, 2)
X(c,k)class throughput at center .
NOTES
If the function call specifies the visit ratios V, class switching is not allowed. If the function call specifies the routing probability matrix P, then class switching is allowed; however, all nodes are restricted to be fixed rate servers or delay centers: multiple-server and general load-dependent centers are not supported. Note that the meaning of parameter lambda is different from one case to the other (see below).
REFERENCES
- Edward D. Lazowska, John Zahorjan, G. Scott Graham, and Kenneth C. Sevcik, Quantitative System Performance: Computer System Analysis Using Queueing Network Models, Prentice Hall, 1984. http://www.cs.washington.edu/homes/lazowska/qsp/. In particular, see section 7.4.1 ("Open Model Solution Techniques").
See also: qnopen, qnos, qnomvisits
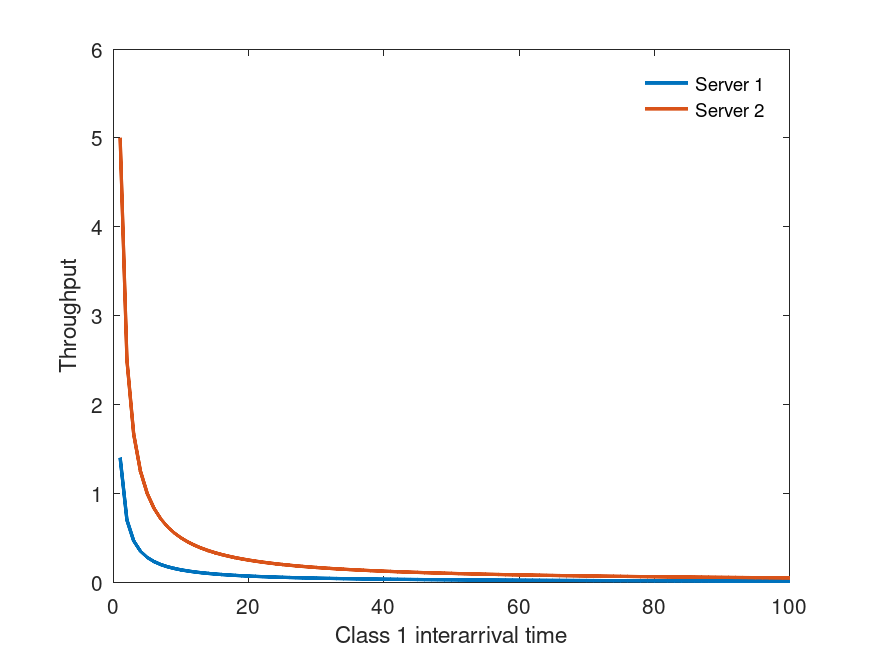
Example: 1
P = zeros(2,2,2,2);
lambda = zeros(2,2);
S = zeros(2,2);
P(1,1,2,1) = P(1,2,2,1) = 0.2;
P(1,1,2,2) = P(2,2,2,2) = 0.8;
S(1,1) = S(1,2) = 0.1;
S(2,1) = S(2,2) = 0.05;
rr = 1:100;
Xk = zeros(2,length(rr));
for r=rr
lambda(1,1) = lambda(1,2) = 1/r;
[U R Q X] = qnom(lambda,S,P);
Xk(:,r) = sum(X,1)';
endfor
plot(rr,Xk(1,:),";Server 1;","linewidth",2, ...
rr,Xk(2,:),";Server 2;","linewidth",2);
legend("boxoff");
xlabel("Class 1 interarrival time");
ylabel("Throughput");
|