Function Reference: qncsmva
- Function File: [U, R, Q, X, G] = qncsmva (N, S, V)
- Function File: [U, R, Q, X, G] = qncsmva (N, S, V, m)
- Function File: [U, R, Q, X, G] = qncsmva (N, S, V, m, Z)
Analyze closed, single class queueing networks using the exact Mean Value Analysis (MVA) algorithm.
The following queueing disciplines are supported: FCFS, LCFS-PR, PS
and IS (Infinite Server). This function supports fixed-rate service
centers or multiple server nodes. For general load-dependent service
centers, use the function qncsmvald instead.
Additionally, the normalization constant , is computed; can be used in conjunction with the BCMP theorem to compute steady-state probabilities.
INPUTS
-
N
Population size (number of requests in the system, N ≥ 0).
If N == 0, this function returns
U = R = Q = X = 0
S(k) mean service time at center (S(k) ≥ 0).
V(k) average number of visits to service center (V(k) ≥ 0).
Z External delay for customers (Z ≥ 0). Default is 0.
m(k) number of servers at center (if m is a scalar, all
centers have that number of servers). If m(k) < 1,
center is a delay center (IS); otherwise it is a regular
queueing center (FCFS, LCFS-PR or PS) with m(k)
servers. Default is m(k) = 1 for all (each
service center has a single server).
OUTPUTS
-
U(k)
If is a FCFS, LCFS-PR or PS node (m(k) ≥
1), then U(k) is the utilization of center ,
. If is an IS node
(m(k) < 1), then U(k) is the defined as X(k)*S(k). In this case the
value of U(k) may be greater than one.
R(k) center response time. The at center
is R(k) * V(k). The system response
time Rsys can be computed either as Rsys =
N/Xsys - Z or as Rsys =
dot(R,V)
Q(k) average number of requests at center . The number of
requests in the system can be computed either as
sum(Q), or using the formula
N-Xsys*Z.
X(k) center throughput. The system throughput Xsys can be
computed as Xsys = X(1) / V(1)
G(n) Normalization constants. G(n+1) contains the value of
the normalization constant , as
array indexes in Octave start from 1. can be used in
conjunction with the BCMP theorem to compute steady-state
probabilities.
NOTES
In presence of load-dependent servers (i.e., if m(k)>1
for some ), the MVA algorithm is known to be numerically
unstable. This issue manifests itself as negative values for the
response times or utilizations. This is not a problem of the
queueing toolbox, but an intrinsic limitation of MVA.
This implementation prints a warning if numerical problems are
detected; the warning can be disabled with the command
warning("off", "qn:numerical-instability").
For product-form QNs with a single load-dependent server
you may want to try the Conditional MVA algorithm
implemented in qncscmva.
REFERENCES
- M. Reiser and S. S. Lavenberg, Mean-Value Analysis of Closed Multichain Queuing Networks, Journal of the ACM, vol. 27, n. 2, April 1980, pp. 313–322. 10.1145/322186.322195
This implementation is described in R. Jain , The Art of Computer Systems Performance Analysis, Wiley, 1991, p. 577. Multi-server nodes are treated according to G. Bolch, S. Greiner, H. de Meer and K. Trivedi, Queueing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications, Wiley, 1998, Section 8.2.1, "Single Class Queueing Networks".
Example: 1
S = [ 0.125 0.3 0.2 ];
V = [ 16 10 5 ];
N = 20;
m = ones(1,3);
Z = 4;
[U R Q X] = qncsmva(N,S,V,m,Z);
X_s = X(1)/V(1); # System throughput
R_s = dot(R,V); # System response time
printf("\t Util Qlen RespT Tput\n");
printf("\t-------- -------- -------- --------\n");
for k=1:length(S)
printf("Dev%d\t%8.4f %8.4f %8.4f %8.4f\n", k, U(k), Q(k), R(k), X(k) );
endfor
printf("\nSystem\t %8.4f %8.4f %8.4f\n\n", N-X_s*Z, R_s, X_s );
Util Qlen RespT Tput
-------- -------- -------- --------
Dev1 0.6665 1.9906 0.3733 5.3319
Dev2 0.9997 16.1767 4.8543 3.3325
Dev3 0.3332 0.4997 0.2999 1.6662
System 18.6670 56.0156 0.3332
|
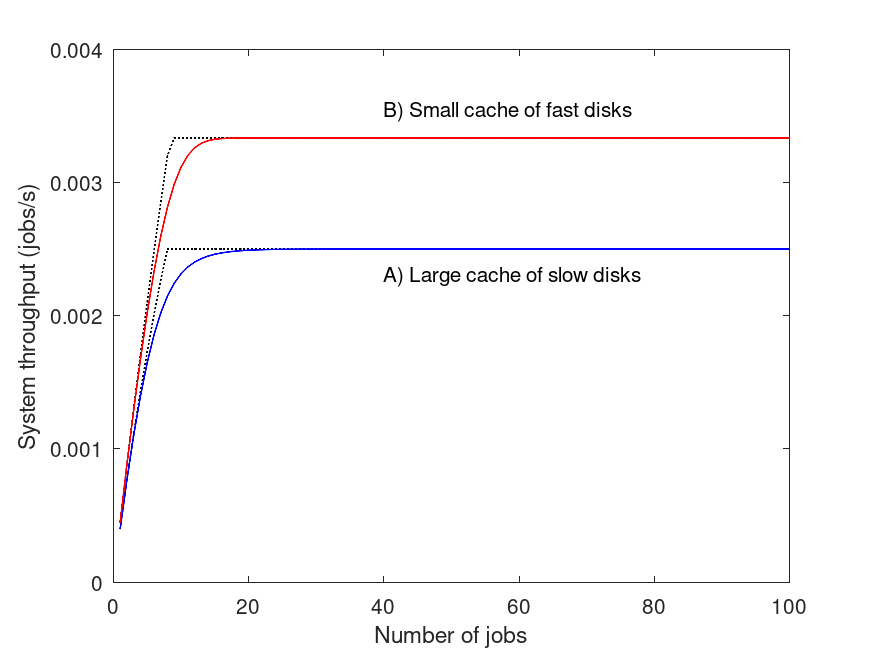
Example: 2
SA = [300 40];
p = .9; P = [ 0 1; 1-p p ];
VA = qncsvisits(P);
SB = [300 30];
p = .75; P = [ 0 1; 1-p p ];
VB = qncsvisits(P);
Z = 1800;
NN = 1:100;
XA = XB = XA_mva = XB_mva = zeros(size(NN));
for n=NN
[nc XA(n)] = qncsbsb(n, SA, VA, 1, Z);
[U R Q X] = qncsmva(n, SA, VA, 1, Z);
XA_mva(n) = X(1)/VA(1);
[nc XB(n)] = qncsbsb(n, SB, VB, 1, Z);
[U R Q X] = qncsmva(n, SB, VB, 1, Z);
XB_mva(n) = X(1)/VB(1);
endfor
plot(NN, XA, ":k", "linewidth", 1,
NN, XA_mva, "-b", "linewidth", 1,
NN, XB, ":k", "linewidth", 1,
NN, XB_mva, "-r", "linewidth", 1);
idx = 40;
displ = 2e-4;
text( NN(idx), XA(idx)-displ, "A) Large cache of slow disks");
text( NN(idx), XB(idx)+displ, "B) Small cache of fast disks");
ax = axis();
ax(3) = 0;
ax(4) = 1.2*max([XA XB]);
axis(ax);
xlabel("Number of jobs");
ylabel("System throughput (jobs/s)");
|