Function Reference: qncsbsb
- Function File: [Xl, Xu, Rl, Ru] = qncsbsb (N, D)
- Function File: [Xl, Xu, Rl, Ru] = qncsbsb (N, S, V)
- Function File: [Xl, Xu, Rl, Ru] = qncsbsb (N, S, V, m)
- Function File: [Xl, Xu, Rl, Ru] = qncsbsb (N, S, V, m, Z)
Compute Balanced System Bounds on system throughput and response time for closed, single-class networks with service centers.
INPUTS
-
N
number of requests in the system (scalar, N ≥ 0).
D(k) service demand at center (D(k) ≥ 0).
S(k) mean service time at center (S(k) ≥ 0).
V(k) average number of visits to center (V(k)
≥ 0). Default is 1.
m(k) number of servers at center . This function supports
m(k) = 1 only (single-eserver FCFS nodes); this
parameter is only for compatibility with qncsaba. Default is
1.
Z External delay (Z ≥ 0). Default is 0.
OUTPUTS
-
Xl -
Xu
Lower and upper bound on the system throughput.
RlRuLower and upper bound on the system response time.
REFERENCES
- Edward D. Lazowska, John Zahorjan, G. Scott Graham, and Kenneth C. Sevcik, Quantitative System Performance: Computer System Analysis Using Queueing Network Models, Prentice Hall, 1984. http://www.cs.washington.edu/homes/lazowska/qsp/. In particular, see section 5.4 ("Balanced Systems Bounds").
See also: qncmbsb
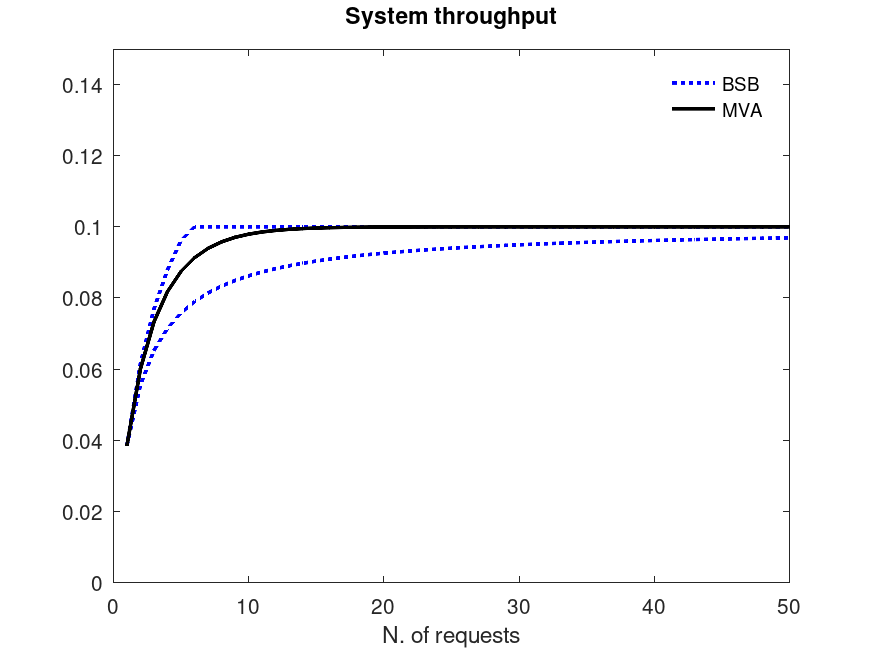
Example: 1
S = [10 7 5 4];
NN = 50;
Xl = Xu = Xmva = zeros(1,NN);
for n=1:NN
[Xl(n) Xu(n)] = qncsbsb(n,S);
[na na na X] = qncsmva(n,S,ones(size(S)));
Xmva(n) = X(1);
endfor
plot(1:NN, Xl, ":b", "linewidth", 2, ...
1:NN, Xu, ":b;BSB;", "linewidth", 2, ...
1:NN, Xmva, "k;MVA;", "linewidth", 2);
xlabel("N. of requests");
ylim([0, 0.15]);
title("System throughput"); legend("boxoff");
legend("location", "northeast");
|