Function Reference: dtmcmtta

Function File: [t N B] = dtmcmtta (P)
Function File: [t N B] = dtmcmtta (P, p0)

Compute the expected number of steps before absorption for a DTMC with state space 1, …, N and transition probability matrix P.

INPUTS

P(i,j)

N \times N transition probability matrix. P(i,j) is the transition probability from state i to state j.

p0(i)

Initial state occupancy probabilities (vector of length N).

OUTPUTS

t
t(i)

When called with a single argument, t is a vector of length N such that t(i) is the expected number of steps before being absorbed in any absorbing state, starting from state i; if i is absorbing, t(i) = 0. When called with two arguments, t is a scalar, and represents the expected number of steps before absorption, starting from the initial state occupancy probability p0.

N(i)
N(i,j)

When called with a single argument, N is the N \times N fundamental matrix for P. N(i,j) is the expected number of visits to transient state j before absorption, if the system started in transient state i. The initial state is counted if i = j. When called with two arguments, N is a vector of length N such that N(j) is the expected number of visits to transient state j before absorption, given initial state occupancy probability P0.

B(i)
B(i,j)

When called with a single argument, B is a N \times N matrix where B(i,j) is the probability of being absorbed in state j, starting from transient state i; if j is not absorbing, B(i,j) = 0; if i is absorbing, B(i,i) = 1 and B(i,j) = 0 for all i \neq j. When called with two arguments, B is a vector of length N where B(j) is the probability of being absorbed in state j, given initial state occupancy probabilities p0.

REFERENCES

  • Grinstead, Charles M.; Snell, J. Laurie (July 1997). Introduction to Probability, Ch. 11: Markov Chains. American Mathematical Society. ISBN 978-0821807491.

See also: ctmcmtta

Example: 1

  

 n = 6;
 P = zeros(101,101);
 for j=0:(100-n)
   i=1:n;
   P(1+j,1+j+i) = 1/n;
 endfor
 for j=(101-n):100
   P(1+j,1+j) = (n-100+j)/n;
 endfor
 for j=(101-n):100
   i=1:(100-j);
   P(1+j,1+j+i) = 1/n;
 endfor
 Pstar = P;
 ## setup snakes and ladders
 SL = [ 1 38;   4 14;   9 31;  16  6;  21 42; ...
       28 84;  36 44;  47 26;  49 11;  51 67; ...
       56 53;  62 19;  64 60;  71 91;  80 100; ...
       87 24;  93 73;  95 75;  98 78 ];
 for ii=1:rows(SL);
   i = SL(ii,1);
   j = SL(ii,2);
   Pstar(1+i,:) = 0;
   for k=0:100
     if ( k != i )
       Pstar(1+k,1+j) = P(1+k,1+j) + P(1+k,1+i);
     endif
   endfor
   Pstar(:,1+i) = 0;
 endfor
 Pstar += diag( 1-sum(Pstar,2) );
 # spy(Pstar); pause
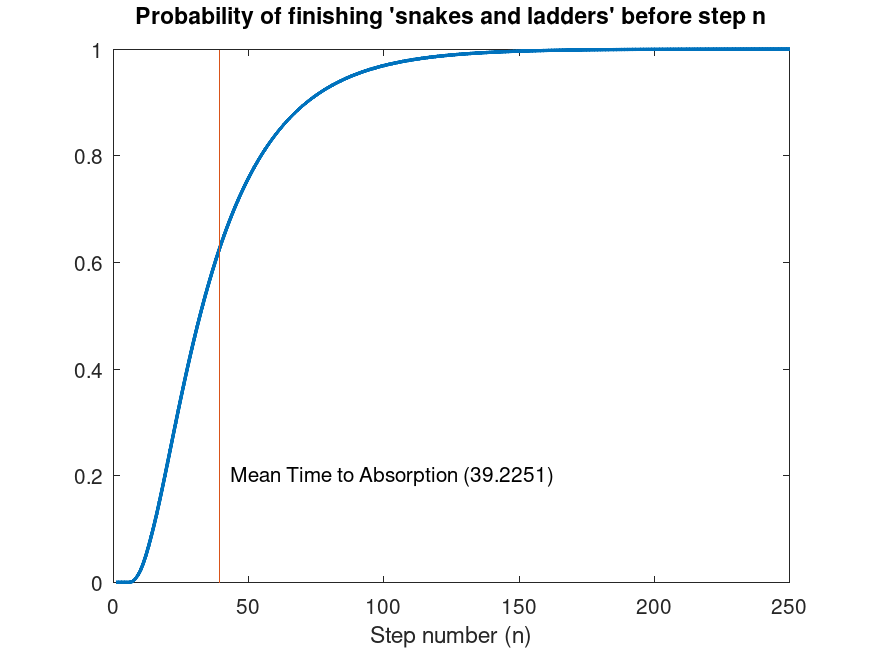
 nsteps = 250; # number of steps
 Pf = zeros(1,nsteps); # Pf(i) = prob. of finishing after step i
 pstart = zeros(1,101); pstart(1) = 1; pn = pstart;
 for i=1:nsteps
   pn = pn*Pstar;
   Pf(i) = pn(101); # state 101 is the ending (absorbing) state
 endfor
 f = dtmcmtta(Pstar,pstart);
 printf("Average n. of steps to complete 'snakes and ladders': %f\n", f );
 plot(Pf,"linewidth",2);
 line([f,f],[0,1]);
 text(f*1.1,0.2,["Mean Time to Absorption (" num2str(f) ")"]);
 xlabel("Step number (n)");
 title("Probability of finishing 'snakes and ladders' before step n");

Average n. of steps to complete 'snakes and ladders': 39.225122
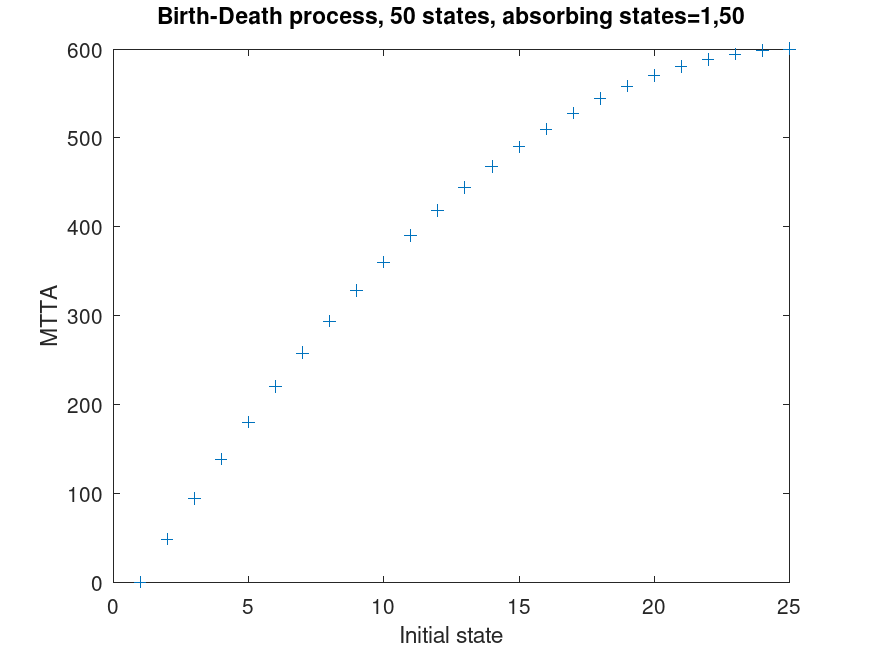
plotted figure

Example: 2

  

 N = 50;
 birth = death = 0.5*ones(1,N-1); birth(1) = death(N-1) = 0;
 P = diag(birth,1)+diag(death,-1);
 P = P + eye(N) - diag(sum(P,2));
 t = zeros(1,N/2);
 initial_state = 1:(N/2);
 for i=initial_state
   p = zeros(1,N); p(i) = 1;
   t(i) = dtmcmtta(P,p);
 endfor
 plot(initial_state,t,"+");
 title(sprintf("Birth-Death process, %d states, absorbing states=1,%d",N,N));
 xlabel("Initial state");
 ylabel("MTTA");
plotted figure