Function Reference: ctmcexps

Function File: L = ctmcexps (Q, t, p )
Function File: L = ctmcexps (Q, p)

With three arguments, compute the expected times L(i) spent in each state i during the time interval [0,t], assuming that the initial occupancy vector is p. With two arguments, compute the expected time L(i) spent in each transient state i until absorption.

Note: In its current implementation, this function requires that an absorbing state is reachable from any non-absorbing state of Q.

INPUTS

Q(i,j)

N \times N infinitesimal generator matrix. Q(i,j) is the transition rate from state i to state j, 1 ≤ i, j ≤ N, i \neq j. The matrix Q must also satisfy the condition \sum_j=1^N Q_i,j = 0 for every i=1, …, N.

t

If given, compute the expected sojourn times in [0,t]

p(i)

Initial occupancy probability vector; p(i) is the probability the system is in state i at time 0, i = 1, …, N

OUTPUTS

L(i)

If this function is called with three arguments, L(i) is the expected time spent in state i during the interval [0,t]. If this function is called with two arguments L(i) is the expected time spent in transient state i until absorption; if state i is absorbing, L(i) is zero.

See also: dtmcexps

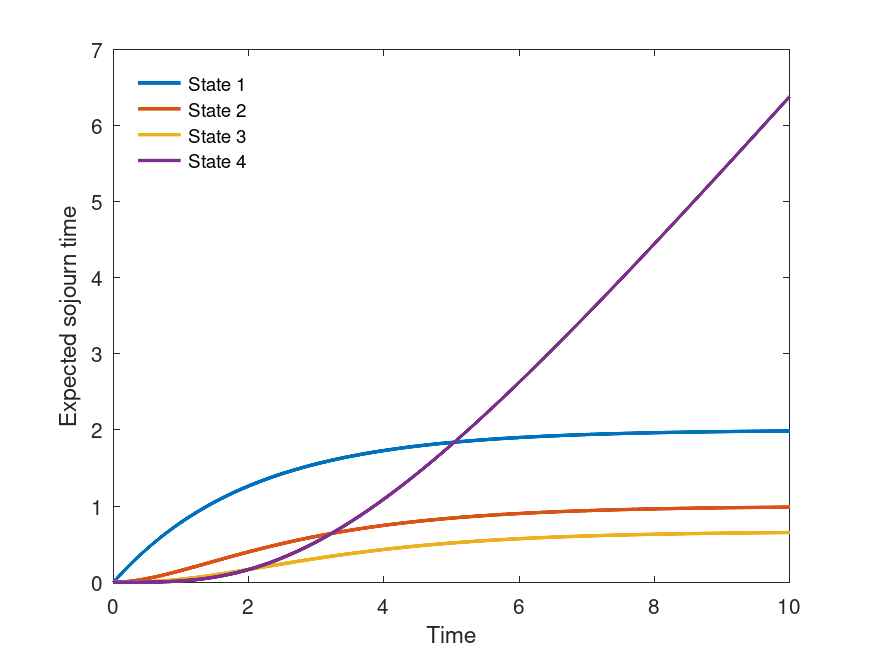
Example: 1

  

 lambda = 0.5;
 N = 4;
 b = lambda*[1:N-1];
 d = zeros(size(b));
 Q = ctmcbd(b,d);
 t = linspace(0,10,100);
 p0 = zeros(1,N); p0(1)=1;
 L = zeros(length(t),N);
 for i=1:length(t)
   L(i,:) = ctmcexps(Q,t(i),p0);
 endfor
 plot( t, L(:,1), ";State 1;", "linewidth", 2, ...
       t, L(:,2), ";State 2;", "linewidth", 2, ...
       t, L(:,3), ";State 3;", "linewidth", 2, ...
       t, L(:,4), ";State 4;", "linewidth", 2 );
 legend("location","northwest"); legend("boxoff");
 xlabel("Time");
 ylabel("Expected sojourn time");
plotted figure

Example: 2

  

 lambda = 0.5;
 N = 4;
 b = lambda*[1:N-1];
 d = zeros(size(b));
 Q = ctmcbd(b,d);
 p0 = zeros(1,N); p0(1)=1;
 L = ctmcexps(Q,p0);
 disp(L);

   2.0000   1.0000   0.6667        0