Function Reference: ctmc

Function File: p = ctmc (Q)
Function File: p = ctmc (Q, t, p0)

Compute stationary or transient state occupancy probabilities for a continuous-time Markov chain.

With a single argument, compute the stationary state occupancy probabilities p(1), …, p(N) for a continuous-time Markov chain with finite state space 1, …, N and N \times N infinitesimal generator matrix Q. With three arguments, compute the state occupancy probabilities p(1), …, p(N) that the system is in state i at time t, given initial state occupancy probabilities p0(1), …, p0(N) at time 0.

INPUTS

Q(i,j)

Infinitesimal generator matrix. Q is a N \times N square matrix where Q(i,j) is the transition rate from state i to state j, for 1 ≤ i \neq j ≤ N. Q must satisfy the property that \sum_j=1^N Q_i, j = 0

t

Time at which to compute the transient probability (t ≥ 0). If omitted, the function computes the steady state occupancy probability vector.

p0(i)

probability that the system is in state i at time 0.

OUTPUTS

p(i)

If this function is invoked with a single argument, p(i) is the steady-state probability that the system is in state i, i = 1, …, N. If this function is invoked with three arguments, p(i) is the probability that the system is in state i at time t, given the initial occupancy probabilities p0(1), …, p0(N).

See also: dtmc

Example: 1

  

 Q = [ -1  1; ...
        1 -1  ];
 q = ctmc(Q)

q =

   0.5000   0.5000

Example: 2

  

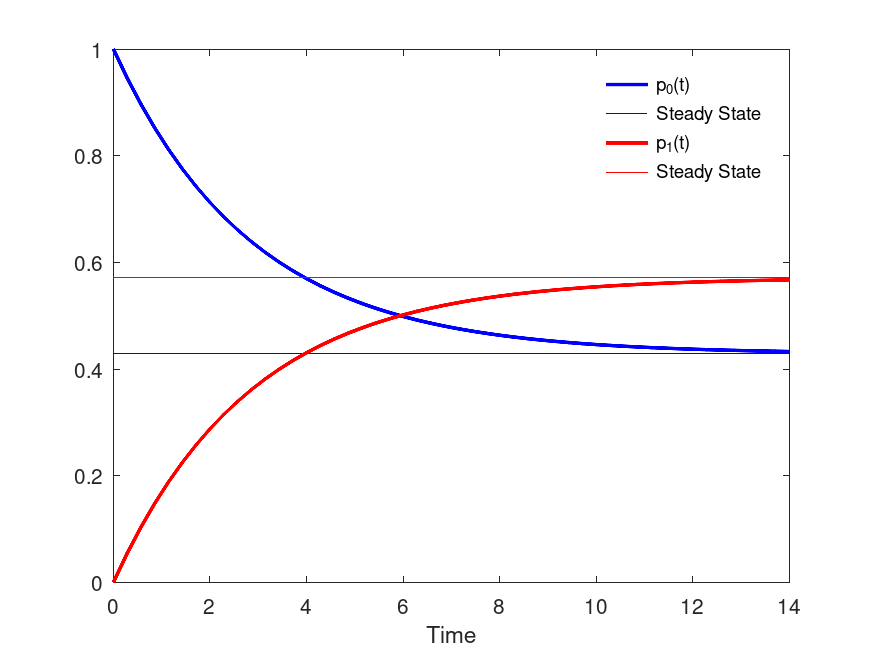
 a = 0.2;
 b = 0.15;
 Q = [ -a a; b -b];
 T = linspace(0,14,50);
 pp = zeros(2,length(T));
 for i=1:length(T)
   pp(:,i) = ctmc(Q,T(i),[1 0]);
 endfor
 ss = ctmc(Q); # compute steady state probabilities
 plot( T, pp(1,:), "b;p_0(t);", "linewidth", 2, ...
       T, ss(1)*ones(size(T)), "b;Steady State;", ...
       T, pp(2,:), "r;p_1(t);", "linewidth", 2, ...
       T, ss(2)*ones(size(T)), "r;Steady State;" );
 xlabel("Time");
 legend("boxoff");
plotted figure

Example: 3

  

 ##
 ## The code below is used in the paper: "M. Marzolla,
 ## "A GNU Octave package for Queueing Networks and Markov Chains analysis"
 ## (submitted to the ACM Transactions on Mathematical Software)
 ## to analyze the reliability model from Figure 2. The model
 ## has been originally described in the paper:
 ##
 ## David I. Heimann, Nitin Mittal, Kishor S. Trivedi, "Availability
 ## and Reliability Modeling for Computer Systems",
 ## Marshall C. Yovits (Ed.), Advances in Computers, Elsevier, Volume 31,
 ## 1990, Pages 175-233, ISSN 0065-2458, ISBN 9780120121311, DOI
 ## https://doi.org/10.1016/S0065-2458(08)60154-0. sep 1989, section
 ## 2.5.

 mm = 60; hh = 60*mm; dd = 24*hh; yy = 365*dd;
 a = 1/(10*mm);    # 1/a = duration of reboot (10 min)
 b = 1/30;         # 1/b = reconfiguration time (30 sec)
 g = 1/(5000*hh);  # 1/g = processor MTTF (5000 h)
 d = 1/(4*hh);     # 1/d = processor MTTR (4 h)
 c = 0.9;          # recovery probability
 [TWO,RC,RB,ONE,ZERO] = deal(1,2,3,4,5);
 ##      2    RC      RB        1     0
 Q = [ -2*g  2*c*g 2*(1-c)*g    0     0; ...  # 2
         0    -b       0        b     0; ...  # RC
         0     0      -a        a     0; ...  # RB
         d     0       0     -(g+d)   g; ...  # 1
         0     0       0        d    -d];     # 0
 p = ctmc(Q);

 disp("minutes/year spent in RC");
 p(RC)*yy/mm  # minutes/year spent in RC
 disp("minutes/year spent in RB");
 p(RB)*yy/mm  # minutes/year spent in RB
 disp("minutes/year spent in 0");
 p(ZERO)*yy/mm  # minutes/year spent in 0

 Q(ZERO,:) = Q(RB,:) = 0; # make states {0, RB} absorbing
 p0 = [ 1 0 0 0 0 ] ; # initial state occupancy probabiliies
 disp("MTBF (years)");
 MTBF = ctmcmtta(Q, p0) / yy # MTBF (years)

minutes/year spent in RC
ans = 1.5743
minutes/year spent in RB
ans = 3.4984
minutes/year spent in 0
ans = 0.6717
MTBF (years)
MTBF = 2.8376